1 研究背景
2009年《物流业调整和振兴规划》出台,我国物流业进入了高速发展时期。2012年物流业进入了调整和转型期,2014年国家出台了物流业中长期发展规划;截至2014年年底,我国的快递企业包括中国邮政在内总量已经达到1.4万多家,数量之多,增长速度之快,这是其他任何一个行业都没有出现过的[1]。2016年《物流业降本增效专项行动方案(2016—2018年)》出台,2017年物流企业集体上市。物流业的发展实现了从无到有,从整体落后到部分超越的良好发展势头。随着物流市场的逐步扩大和
物流量的逐年增加,集团企业和跨国经营物流企业增多,物流运输跨区域调度的频率越来越高。
2022年我国物流运行情况分析报告显示,2022年我国社会物流总费用与GDP的比率为14.7%,物流总费用为17.8万亿元,其中,运输费用为9.55万亿元,运输成本占社会物流总费用的53.7%。因此,合理地进行运输调度,设计规划最优的运输调度方案是降低物流业总费用的主要途径。
2 服务行业的物流特点
我国是全球最大的服装制造国家,曾有“世界加工厂”的美誉。我国的服装生产与制造在全球服装市场中占据较大的份额,传统的服装行业以线下的批发零售为主要的销售模式。随着互联网和信息技术的发展,服装行业于20世纪90年代进入电子商务领域,最早实现了信息化变革,并积极探索将线上和线下相结合的销售模式。
电子商务的出现和成功应用,催生了一大批电商平台,使得服装行业的营销模式逐渐由商圈营销向社群营销转变,服装营销不再受地域的限制,物流需求呈现出了点多面广的特点。2020年至今,我国每年的快件量都在千亿件以上。中国物流与采购联合会统计数据显示,2022年至今,纺织业、纺织服饰业、食品酒饮和医药制造业商务快件呈持续上升趋势。近年来,随着经济发展和人民消费水平的提升,人们的消费观念发生了巨大变化,个性化、差异化需求越来越明显,对服装的物流需求呈现出了多品种、小批量的特点。
时效性强、需求多样化的服装物流如何响应降本增效方案的落实,同时在市场中保持核心竞争力,成为服装行业的重要研究课题。
3 服装行业常见的运输调度问题及求解方法
对服装业物流从业人员来说,常见的物流运输调度问题有三大类,一是供需平衡的运输调度问题,二是供不应求的运输调度问题,三是供大于求的运输调度问题。三类问题有一个共同的要求,那就是既要按要求满足客户的需求,又要以尽可能低的成本完成调度任务。解决这类问题最常用的方法有西北角法、最小元素法、Excel规划求解方法等。以供需平衡的运输调度问题为例,借助一个例子来说明求解方法。
某种物资有甲、乙、丙三个供应点,有A、B、C、D四个需求点。三个供应点的供应量分别为18件、18件、19件,四个需求点的需求量分别为16件、15件、7件、17件。总供应量和总需求量相等都为55件,这是一个典型的供需平衡运输调度问题。如何安排调运方案,使之能既满足需求又成本最低呢?
3.1 基于西北角法的运输调度解决方案
物流运筹学研究就是在运筹学方法的基础上结合物流的特点,利用运筹学的方法来解决物流过程中的优化管理问题[2]。西北角法是物流运筹学中常用的解决运输调度问题的方法。
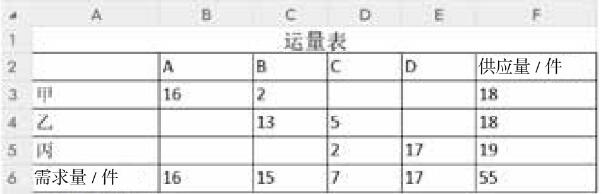
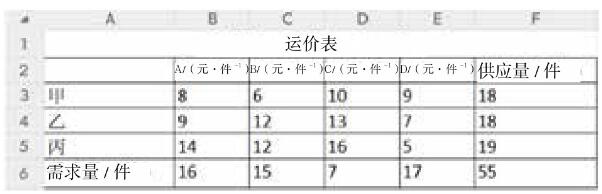
西北角法调运方案设计示例如图1所示,将供应量、需求量及运价设计在一张Excel表格中,西北角法,顾名思义就是在安排调运方案的过程中,首先从西北角即表格的左上角位置安排调运,即优先由甲给A客户送货,甲供应18件,A需要16件,A的需求得到满足,此时甲剩余2件。在此时的表格中,B列不予考虑,左上角单元格更新为C3,由甲给B供货,因为甲仅剩余2件可全部供应给B,甲货物供应完毕,表格中第三行不予考虑。除去B列和第三行之后,此时的表格左上角单元格更新为C4,依次继续完成调运,直到所有的需求均被满足。
图1 西北角法调运方案设计示例
由运量表中产生调运量的单元格与运价表中对应位置的运价相乘再求和,可以得到此调运方案的总运输成本为478元。
3.2 基于最小元素法的运输调度解决方案
第二种可行的调运方法为最小元素法。最小元素法是物流运筹学中用于解决运输问题的一种有效而且简单的方法,该方法与西北角法相比更有效。最小元素法调运方案设计示例如图2所示,这里的最小元素指的是运价的最小值,所谓的最小元素法,即每次安排都是选当前运价表中运价最少的单元格安排调运。当前运价表中最小的元素为E5单元格(5元),就意味着要丙给客户D送货,此时D的需求得到满足,此时D列的运价后续将不予考虑,丙剩余2件货物。运价表中的最小元素为C3单元格(6元),即由甲给B送货成本最低,此时B的需求得到满足,B列的运价后续将不予考虑,甲剩余3件货物。然后在剩余的A、C两列中找最小运价单元格继续安排调运,直到所有的需求均被满足。
由产生调运量的单元格与对应位置的运价相乘再求和,可以得到此调运方案的总运输成本为412元。
图2 最小元素法调运方案设计示例
以上两种方法通过手动计算都得到了可行的调运方案,为完成调运任务提供了依据和参考,保证调运工作的顺利开展,但是两种方案不尽相同,而且最小元素法得到的总运费比西北角法节约了66元。那么,最小元素法是不是解决运输调度问题的最优方法呢?下面进一步分析。
3.3 基于Excel规划求解工具的运输调度解决方案
随着2017年物流业降本增效行动方案的出台,物流业的作业效率亟待提升。大数据云计算物联网等技术在物流领域的应用越来越广泛,对物流从业人员的信息素养和信息化数据分析能力的要求越来越高。目前,进行数据分析与处理方面的软件有很多,如Python、Matlab、Oringe、Spss、Excel等。其中,Microsoft Excel以其使用的普遍性、强大的数据分析与处理功能被广泛使用。
运输调度问题实际上是在若干资源有限的情况下如何找到最优的决策的问题,这类问题属于典型的运筹学问题。Excel软件中的规划求解加载项是解决运筹学问题的工具。用Excel规划求解工具寻找最优解,最重要的是正确地提炼出规划求解的三要素。规划求解工具的三要素为目标单元格、可变区域和约束条件。以上述案例为例,从西北角法和最小元素法求解过程可以看出,不同的方法得到不同的调运量表,运量表中的单元格即可变单元格。目标单元格为总运价。总运价为调运量与运价表中对应单元格的乘积之和,这个计算可以用Excel中的SUMPRODUCT()函数实现。该函数可以实现在给定的几组数组中,将数组中对应的元素相乘,并返回乘积之和。
对供需平衡的调运问题来说,总的供应量应该等于总的需求量,各个需求点的需求均应该被满足,各个供应点的供应量也应该全部供应完毕。因此,约束条件就是运量表中每个供应点的实际供应量之和应该等于运价表中各供应点的最大供应量,而每个需求点的实际需求量之和等于运价表中设定的最大需求量。约束条件可以通过Excel函数的SUM()函数计算完成。
单元格设置完成之后,点开Excel的规划求解加载项,打开对话窗口在对应位置填入内容。因为要寻求的是使总运输成本最低的调运方案,故设置取目标函数的最小值。选择的求解方法为单纯的线性规划后即可求解。该方法得到的总运价为407元,比最小元素法节省成本5元。不仅完成了调运任务,还使总费用最低,因此该方案最优。
“规划求解”通过调整决策变量单元格中的值以满足约束单元格上的限制,并产生对目标单元格期望的结果。用Microsoft Excel中的“规划求解”可以解决线性规划与非线性规划中的优化问题,还应用于数学模型拟合过程中的参数优化、单变量求解等方面[3]。
3.4 用Excel规划求解工具来解决供需不平衡的调度问题
在实际的服装运输调度工作中,往往会遇到供需不平衡的情况。供不应求或者供大于求的情况都是服装行业物流人员常见的运输调度问题[4]。解决这类问题的基本思路就是将供需不平衡的问题转化为供需平衡的问题,再利用Excel规划求解的工具来得到最优方案。
举例说明,有三个供应点甲、乙、丙向四个需求点A、B、C、D供应物资,四个需求点每日的物资需求量分别为16件、30件、24件、30件,三个供应点的每日物资供应量分别为30件、40件、50件,运费确定的情况下试确定最经济的物资运输方案。
从已知数据可以看出,三个供应点的总产量为120件,四个需求点的总需求量为100件,显然这是一个供大于求的调运问题。对于这类运输调度问题,可以采取增加一个虚拟的需求点E,从而将供需不平衡的问题转化为供需平衡的问题来求解。设虚拟需求点E的需求量为20件,进而利用Excel的规划求解工具求最优解。
因为目标是要求总调运成本最低的解决方案。既然E点是一个虚拟的需求地,也就是这个E点不会产生实际需求,所以可以将E点的运价设定为无穷大,然后按照供需平衡的调运问题进行求解,即文中3.2部分。
4 小结与展望
相关统计资料数据显示,物流业的总成本有60%~70%花费在仓储运输环节。物流运输调度方案的制订是物流活动的重要环节,在人力劳动为主的物流1.0时代,这项工作都是依靠人工手动来完成的,但是通过人工调度的方式往往无法兼顾多种约束条件,也无法判断调度结果是否满足要求,不仅耗时耗力,还容易导致调度出现任务工作不均匀、人员任务不饱和的情况,缺乏科学性和经济性的论证,根本无法实现降本增效的目标。
目前,物流业已经进入以信息化为特征的3.0时代,市面上有很多基于互联网技术研发的调度系统,但由于其研发和购置成本相对较高,无法满足大多数中小服装物流企业的需求。在大数据背景下,借助现代信息技术和数据分析软件,低成本、高效率地完成物资调度,是物流业降本增效的重要突破口[5]。
5 结束语
文章先后利用西北角法、最小元素法和Excel规划求解工具对服装业的运输调度问题进行了分析,可以看出规划求解工具是最行之有效的工具。但是文章只针对供需平衡、供大于求、供不应求三种常见的运输调度问题展开分析,在实际调运过程中,由于市场竞争会导致不稳定因素的出现,往往会遇到供应量或需求量无法明确固定而是处于一个区间范围内的情况,对于这类问题的求解,将在后续的研究中进行分析。